Factoring a trinomial such as ![]() can be tricky. There are several techniques, including inspection, using a grid, and decomposition – also known as ‘splitting the middle’. This page gives some examples of the decomposition technique.
can be tricky. There are several techniques, including inspection, using a grid, and decomposition – also known as ‘splitting the middle’. This page gives some examples of the decomposition technique.
Review when  :
: 
Let’s expand ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}&(x+3)(x+4)\\[10pt]=&x^2+4x+3x+12\\[10pt]=&x^2+7x+12 \end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-aacf571f6e447e2148f0d31b3f10339a_l3.png)
We notice that ![]() gives us the
gives us the ![]() ; and that
; and that ![]() gives us the constant
gives us the constant ![]() .
.
To factor a trinomial of the form ![]() , we need two values
, we need two values ![]() such that
such that ![]() and
and ![]() .
.
Click here to review factoring ![]() .
.
Factor 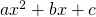 , where
, where 
To factor a trinomial where ![]() we need
we need ![]() and
and ![]() .
.
First, let’s examine the expansion of a factored trinomial of this form:
![Rendered by QuickLaTeX.com \begin{align*}&(3x+2)(x+5)\\[10pt]=&3x^2+15x+2x+10\\[10pt]=&3x^2+17x+10\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-3e254ad3b6f80d740b2f0a4da5d17e59_l3.png)
This time, notice that ![]() as expected, but
as expected, but ![]() . Rather,
. Rather, ![]() .
.
Instead of looking for two numbers that add to 17 and multiply to 10, we need to look for two numbers that add to 17 and multiply to 30.
Example 1:
Factor:
![]()
Look for two numbers, ![]() and
and ![]() , such that
, such that ![]() and
and ![]() .
.
The factor pairs of 40 are: (1,40); (2,20); (4,10); (5, 8)
To make 22, we need to use the pair (2,20).
We write a new line of work:
![Rendered by QuickLaTeX.com \begin{align*}&5x^2+22x+8\\[10pt]=&5x^2+20x+2x+8\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-6c0355ff7a3190d1e994c9109b25aebc_l3.png)
(It doesn’t matter if you write the ![]() first or the
first or the ![]() first).
first).
Now we look for a common factor in the first two terms:
![]()
Perhaps suprisingly, (explained here), let’s look at the last two terms;
![]()
Ha! ![]() is a common factor! Put together we have:
is a common factor! Put together we have:
![Rendered by QuickLaTeX.com \begin{align*}&5x^2+20x+2x+8\\[10pt]=&5x(x+4)+2(x+4)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-71bbfca97e05ca21f182431c1697eaf1_l3.png)
Taking out ![]() as a common factor, we have:
as a common factor, we have:
![Rendered by QuickLaTeX.com \begin{align*}&5x(x+4)+2(x+4)\\[10pt]=&(x+4)(5x+2)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-4ab684db6914a3cb9cf55cd8ea4ff581_l3.png)
Example 2:
![]()
Find two numbers, ![]() and
and ![]() such that
such that ![]() and
and ![]() .
.
Factor pairs of 24 are (1,24); (2,12); (3,8); (4,6). Now ![]() so let
so let ![]() and
and ![]() .
.
Splitting the middle term with ![]() and
and ![]() we have:
we have:
![Rendered by QuickLaTeX.com \begin{align*}&4x^2-5x-6\\[10pt]=&4x^2+3x-8x-6\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-ca9ee536076575469d7fd79f8c7b4687_l3.png)
Grouping we have:
![Rendered by QuickLaTeX.com \begin{align*}&4x^2+3x-8x-6\\[10pt]=&(4x^2+3x)-(8x+6)\\[10pt]=&x(4x+3)-2(4x+3)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-f8a880acfd2717cc45ab9f8262e3fd13_l3.png)
Completing we have
![Rendered by QuickLaTeX.com \begin{align*}&x(4x+3)-2(4x+3)\\[10pt]=&(4x+3)(x-2)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-87b2ab83e1cfc8d0322354e62b75b406_l3.png)
Example 3:
![]()
First, we notice that all three terms share a common factor 3. Let’s factor this out:
![Rendered by QuickLaTeX.com \begin{align*}&6x^2+27x+12\\[10pt]=&3(2x^2+9x+4)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-c323c76a967e21486afcb12bcfb55041_l3.png)
Now we factor the reduced trinomial ![]() ; however the
; however the ![]() is kept present throughout. You might also try factoring without reducing to see how the result compares.
is kept present throughout. You might also try factoring without reducing to see how the result compares.
Now we look for ![]() and
and ![]() such that
such that ![]() , and
, and ![]() .
.
Factor pairs of 8 are (1, 8); (2, 4). To satisfy ![]() , we need to use
, we need to use ![]() and
and ![]() .
.
Splitting the middle term we have
![Rendered by QuickLaTeX.com \begin{align*}&3(2x^2+9x+4)\\[10pt]=&3(2x^2+x+8x+4)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-7cd15947ac781eacf0e85f8f219bea9e_l3.png)
Grouping gives
![Rendered by QuickLaTeX.com \begin{align*}&3(2x^2+x+8x+4)\\[10pt]=&3((2x^2+x)+(8x+4))\\[10pt]=&3(x(2x+1)+4(2x+1))\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-a89e570eff003ca68fc70473285c2b3f_l3.png)
Completing we have
![Rendered by QuickLaTeX.com \begin{align*}&3(x(2x+1)+4(2x+1))\\[10pt]=&3(2x+1)(x+4)\end{align*}](http://tentotwelvemath.com/wp-content/ql-cache/quicklatex.com-d536f7c73083927cc005c0b95cb06cab_l3.png)
Try it out

With help – use the first applet below. No help? Use the second applet.
Correct fields show as green, incorrect as red.
Done here! go back to Number and Algebra menu